Week 4 - Non-Linear Hypothesis and Neural Network (NN)
In previous notes, we introduced linear hypotheses such as linear regression, multivariate linear regression and simple logistic regression. They are useful for many problems, but still not enough to cover all problems in reality. The non-linear classification problems is one of those that can not be solved by just using linear method. So, let’s start!
Non-Linear Classification Problem
When we want to use machine learning to build a car image classifier, we need a training dataset with true labels, a car or not a car. After learning process, we get a good classifier. When we test it with a new image, the classifier will answer whether this new image is a car or not.


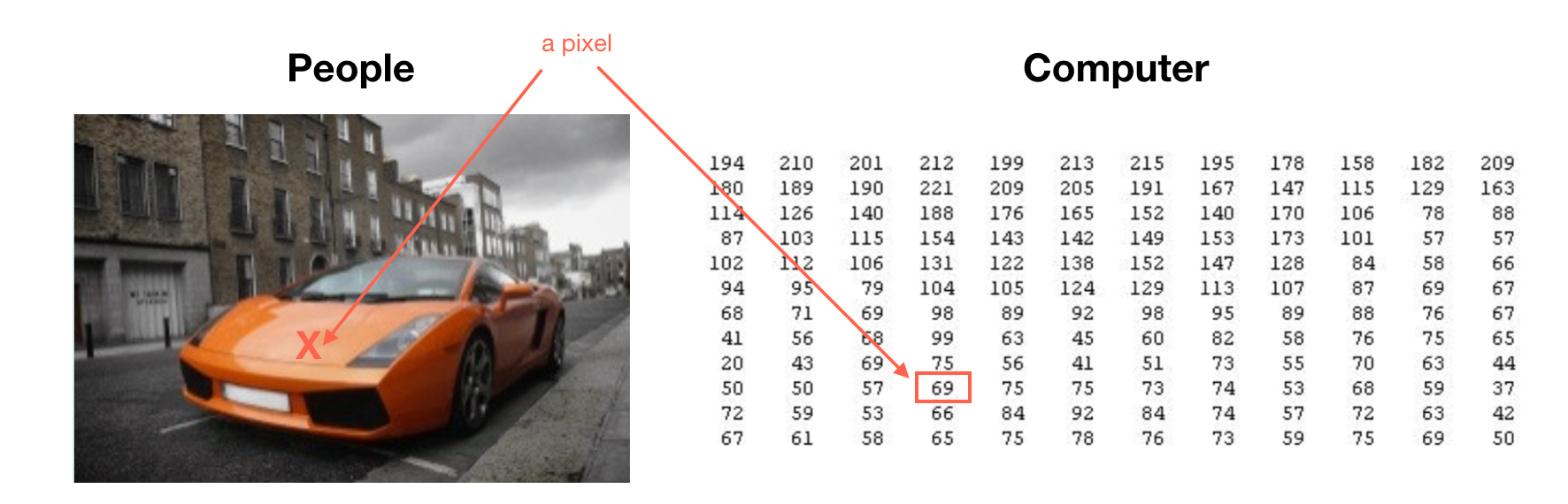
Source: week4 lecture slides, by Andrew Ng Before moving on, we need to know how a computer ‘sees’ a picture. Like the picture in the right, a computer always ‘sees’ an image as a bunch of pixels with intensity values. For example, the picture shows the position of a pixel (red point) and its intensity value is 69.

Source: week4 lecture slides, by Andrew Ng Now, let’s see the learning process. First, take two pixels as features.

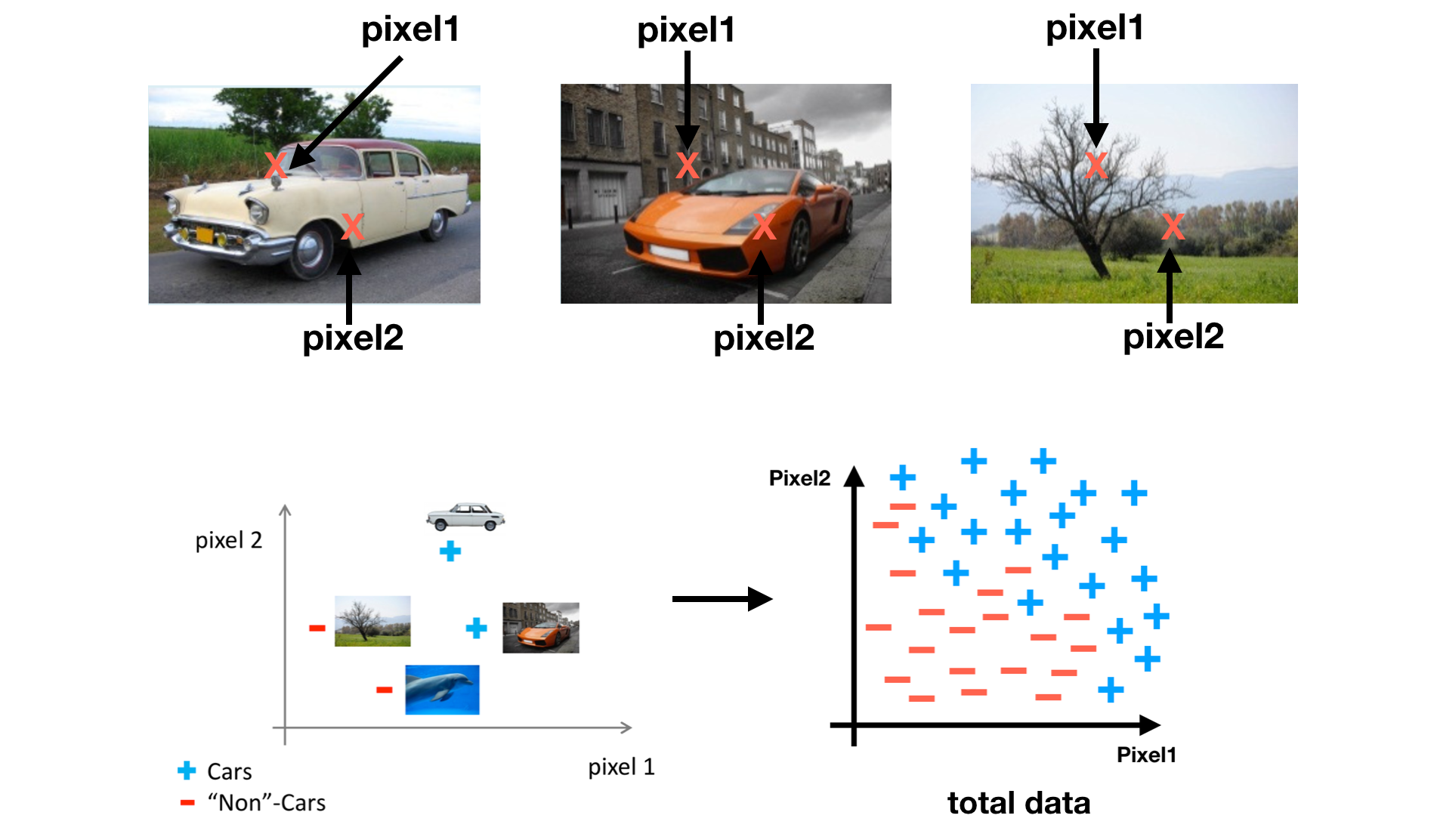
Source: week4 lecture slides, by Andrew Ng Second, define a non-linear logistic regression as a hypothesis H. Our goal is to find a good H which can distinguish positive data and negative data well.

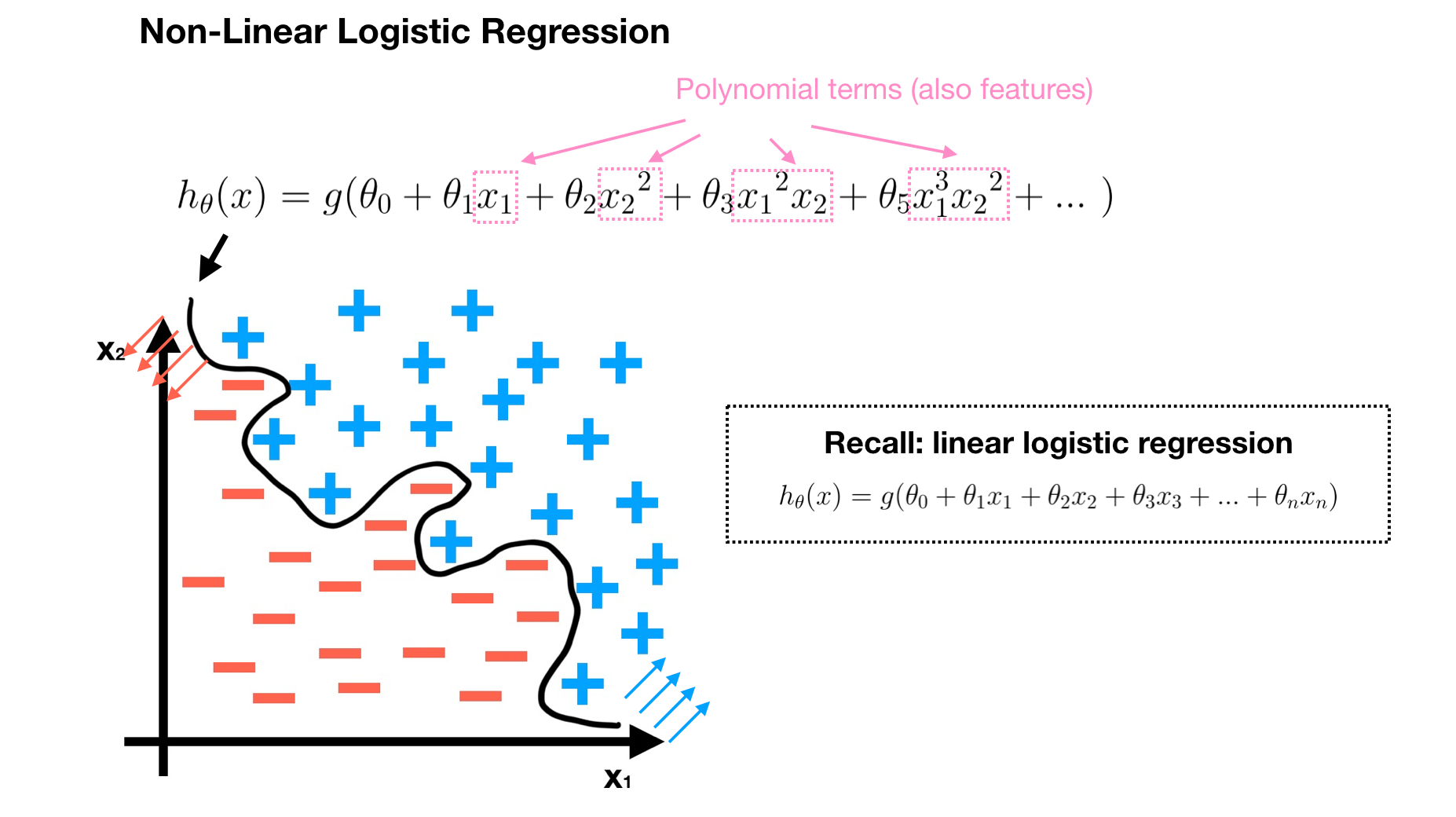
Last, learn all parameters of H. Compare this with linear logistic regression introduced in week3, the non-linear form is more complex since it is with lots of polynomial terms. However, when a number of feature is large, the above solution is not a good choice to learn complex non-linear hypothesis. Suppose we have a 50x50 pixels image and all pixels are features, hence, a non-linear hypothesis must have more than 2500 features since H has extra quadratic or the cubic features. The computation cost would be very expensive in order to find all parameters θ of these features per the training data. Therefore, we need a better way — Neural Network, which is a very powerful and widely used model to learn a complex non-linear hypothesis for many applications.
Neural Network (NN)
In this section, we are going to talking about how to represent hypothesis when using neural networks. Originally, Neural Network is an algorithm inspired by human brain that tries to mimic a human brain. Like human brain’s neurons, NN has a lots of interconnected nodes (a.k.a neurons) which are organized in layers.
Simplest Neural Network
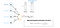
This simplest NN model only contains a neuron. We can treat a neuron (node) as a logistic unit with Sigmoid (logistic) Activation Function, which can output a computation value based on sigmoid activation function.
- The terminology of parameters θ in NN **is called **‘weights’.
- Depending on the problems, you can decide whether to use the bias units or not.
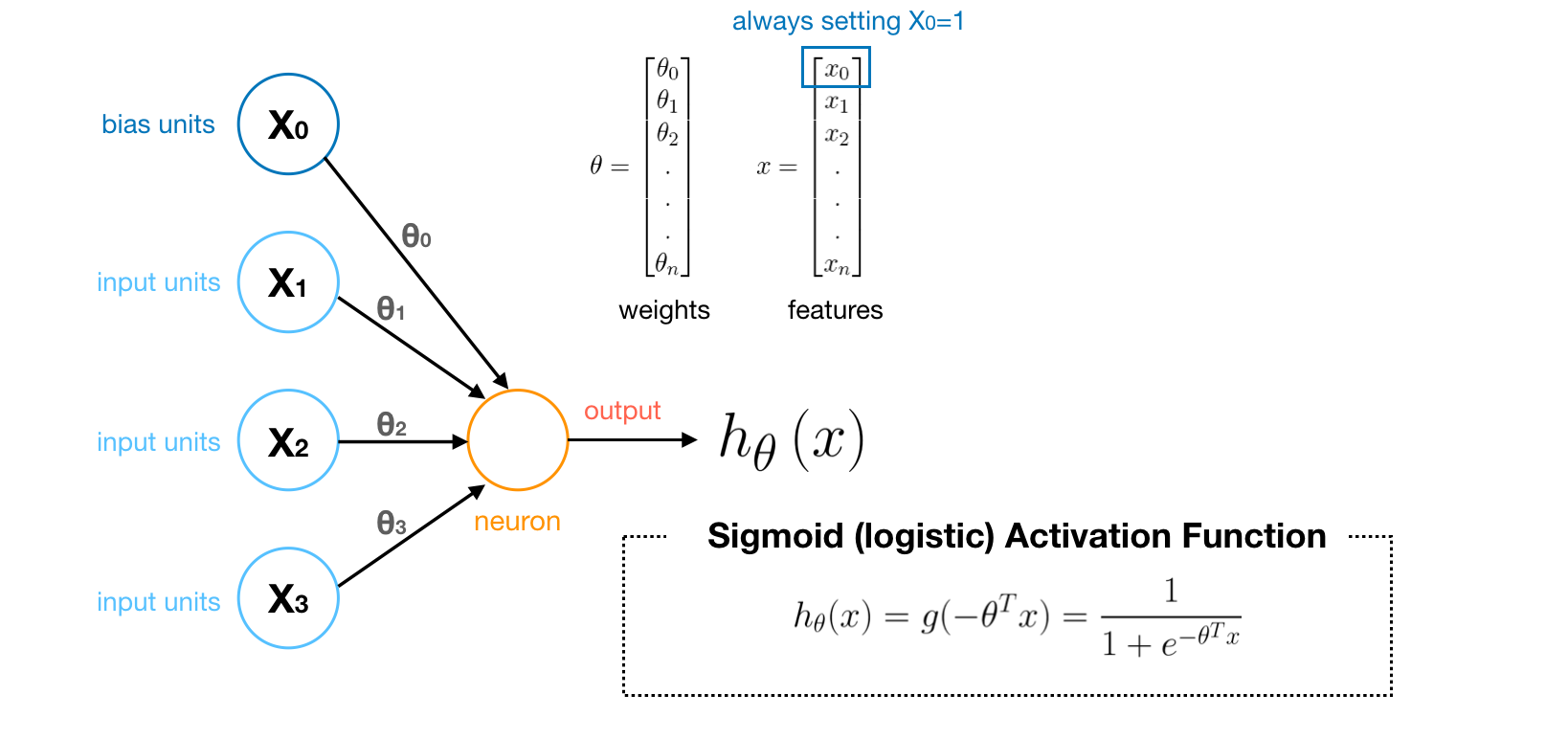
Neural Network (NN)
Layer 1 is called Input Layer that inputs features. Last Layer is called Output Layer that outputs the final value computed by hypothesis H. The layer between Input Layer and Output Layer is called Hidden Layer, which is a block we group neurons together.
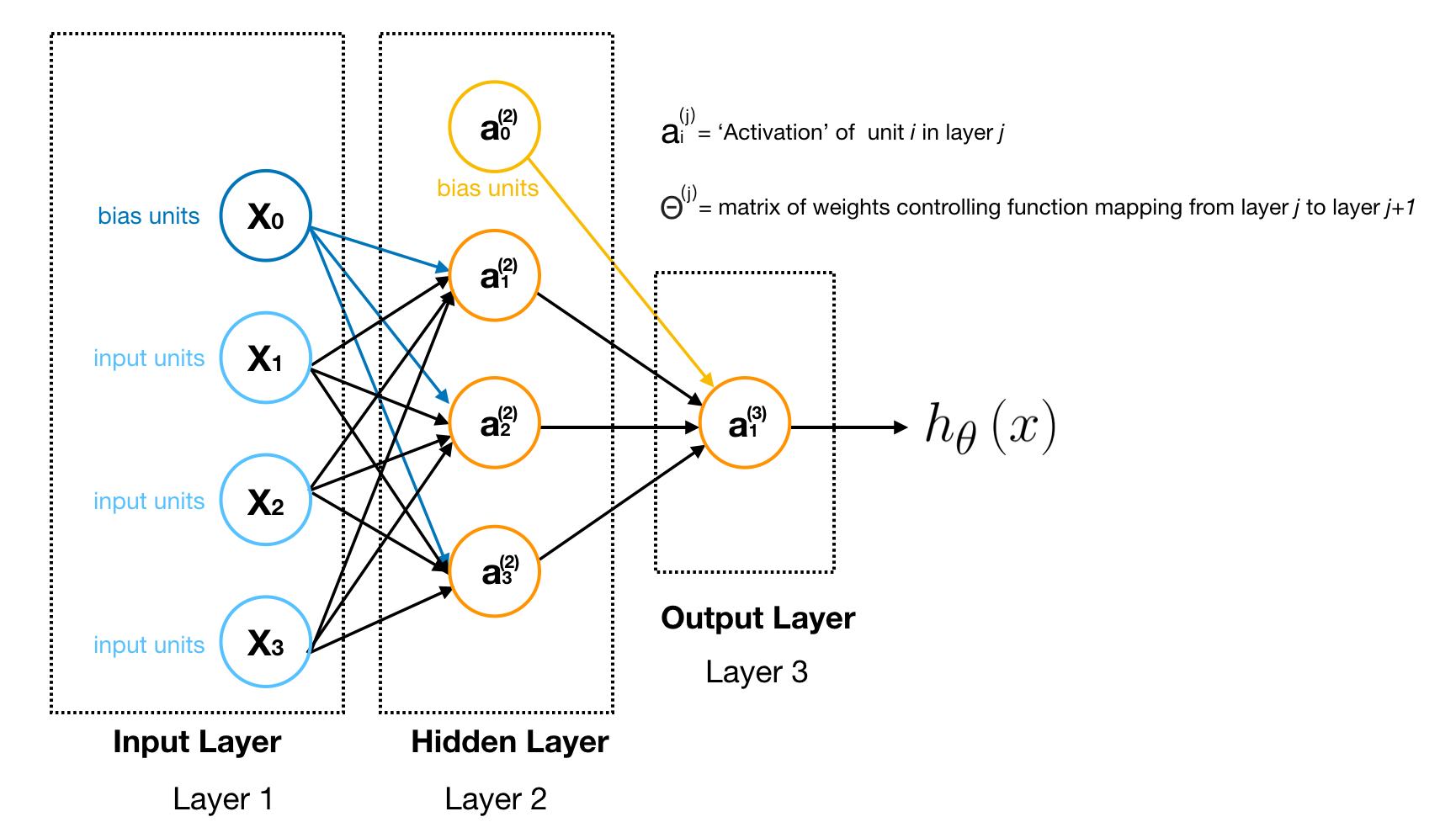
Note
A neuron (node) is actually a logistic unit with Sigmoid (logistic) Activation Function(i.e simple logistic regression). If you are familiar with Linear Algebra, you can think of a hidden layer as a linear combination of previous layer’s nodes. Therefore, the core idea of NN is to solve complex non-linear classification problem by using many sequences of simple logistic regression.
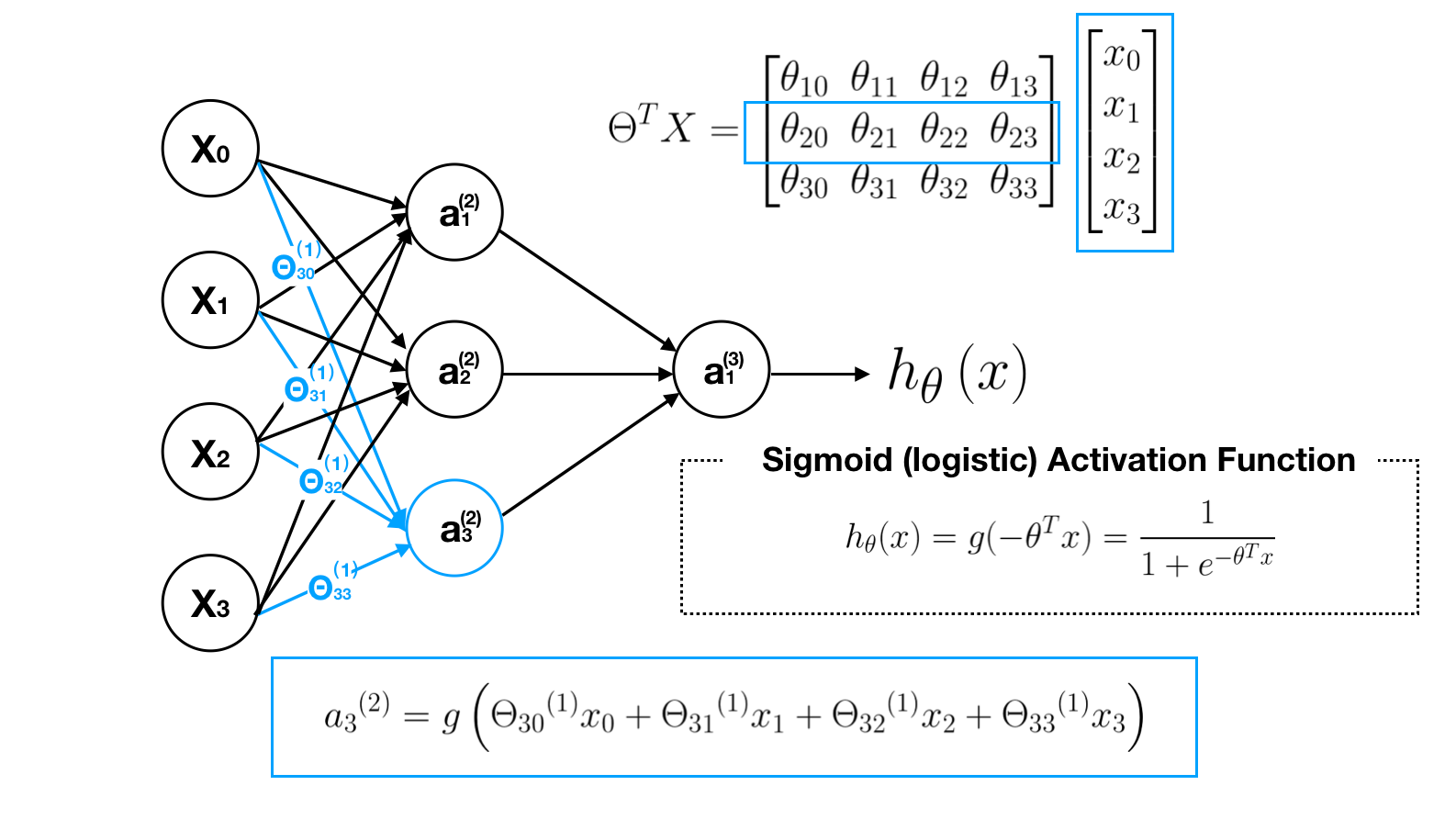
In order to get a clear picture about what this neural network is doing, let’s go through the computational steps and visualize them. First, we visualize the transition process of matrix Θ, which is a controlling function mapping from layer j to j+1.



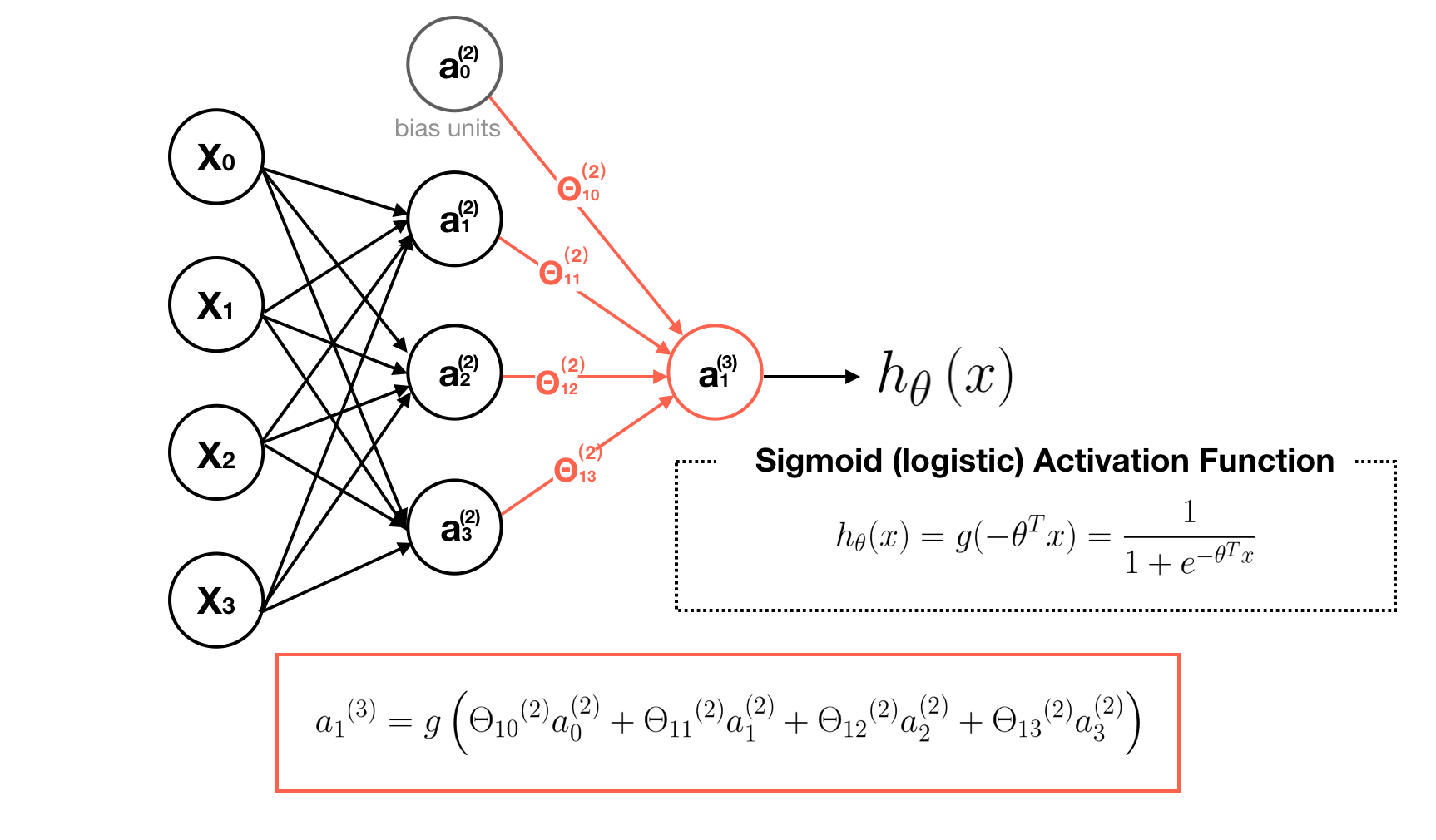
Second, we visualize each computation process of neurons. Note that the output value of each neurons is calculated by its sigmoid activation function.

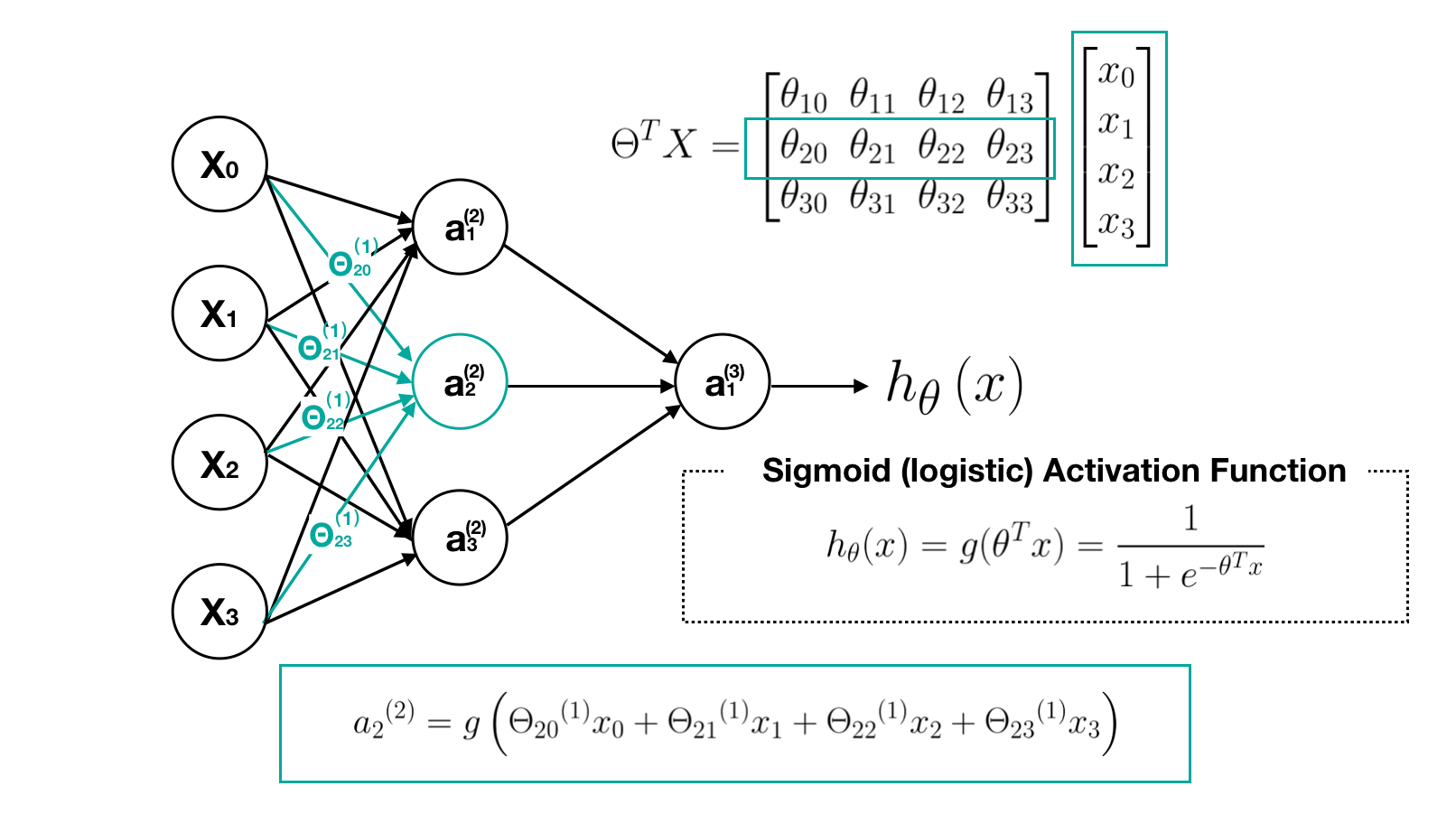

Other Neural Network Architectures
Other Neural Network Architectures can be designed by extending hidden layers. The number of neurons per layer will be based on the problems.

Applications and Examples
Based on above concept, we are going to design some NN to show that how an NN model can be applied to non-linear classification problems.
Examples1 — AND
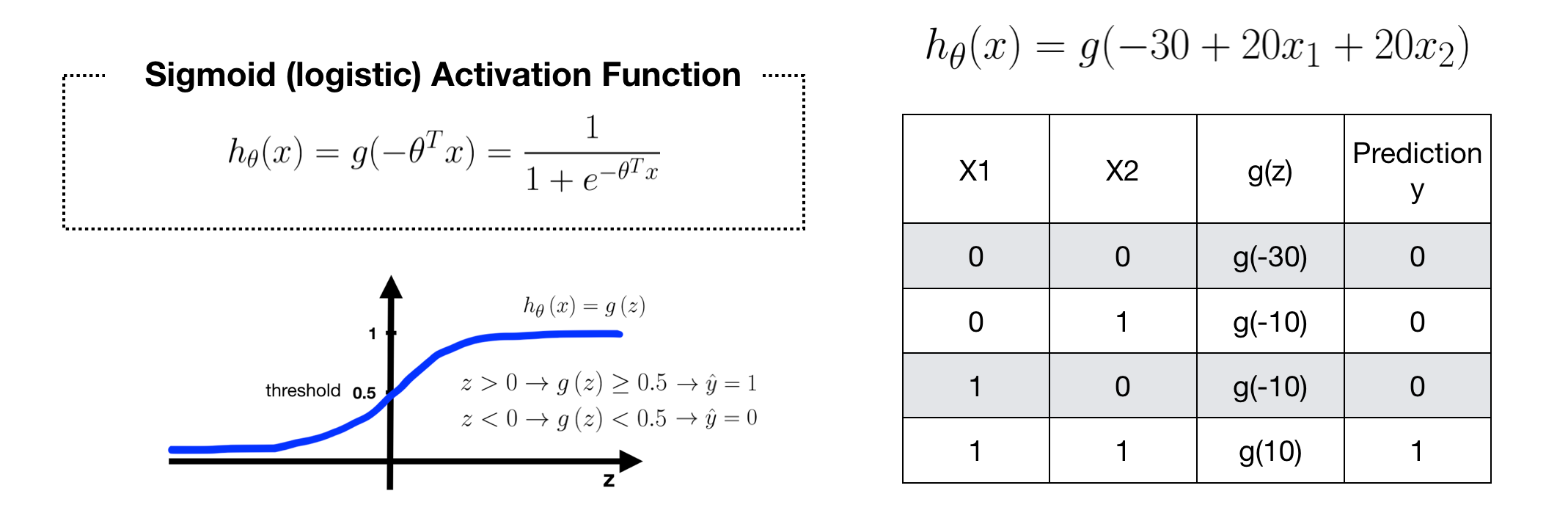
We can design a simple NN with single neuron for solving AND problem. Given -30, 20 and 20 as weights, the Sigmoid Activation Function H of this neuron (node) can be specified. When we predict data using this H, we can get a perfect result.



Examples2 — OR
The concept of OR operation is similar to AND, but we change the weight of the bias unit as -10.



Examples3 — Negation

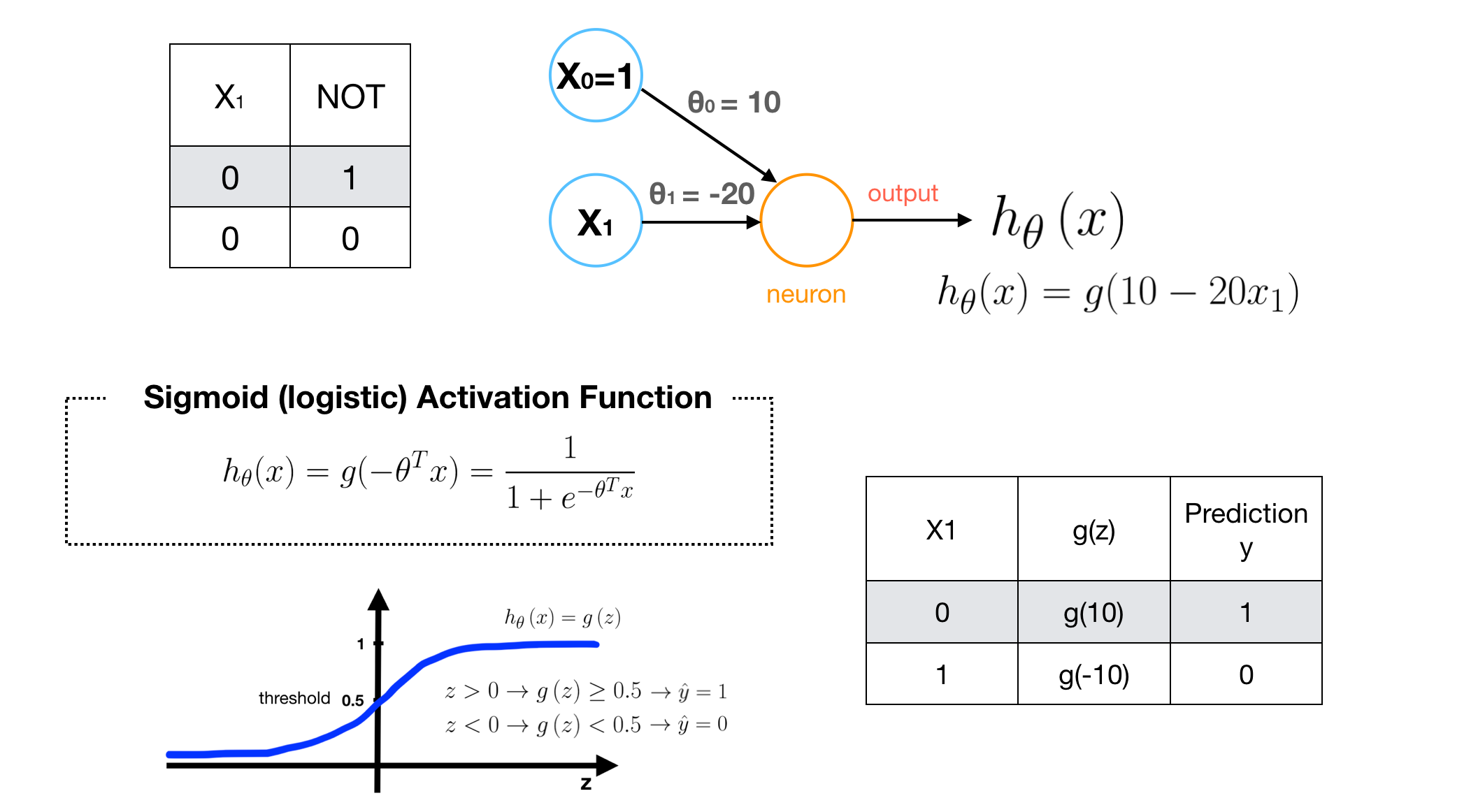
Examples4 — NAND

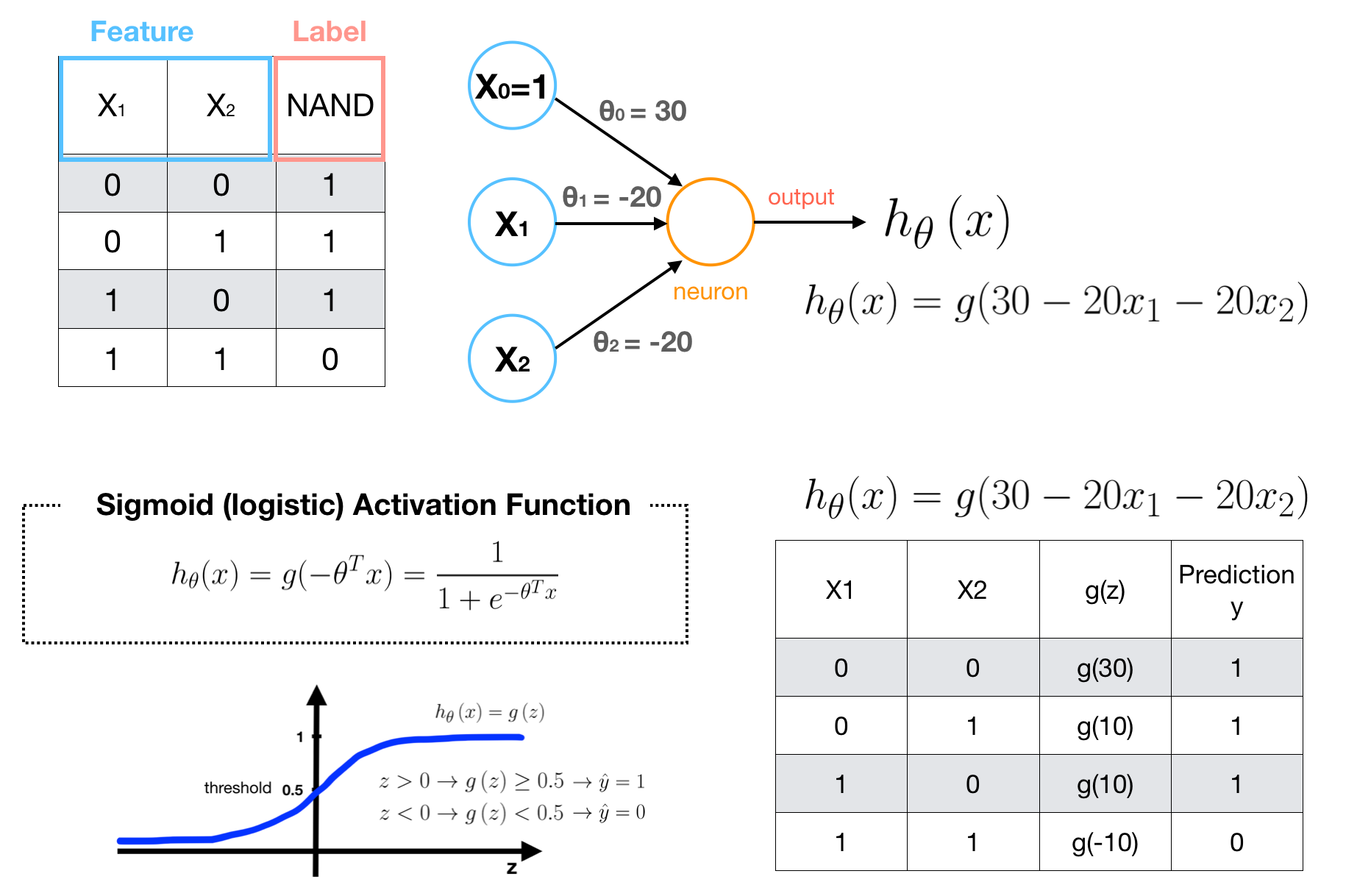
Examples5 — XOR
Clearly, this is a non-linear classification problem, we can solve it by using a non-linear logistic regression **H** **that we discussed in the beginning.

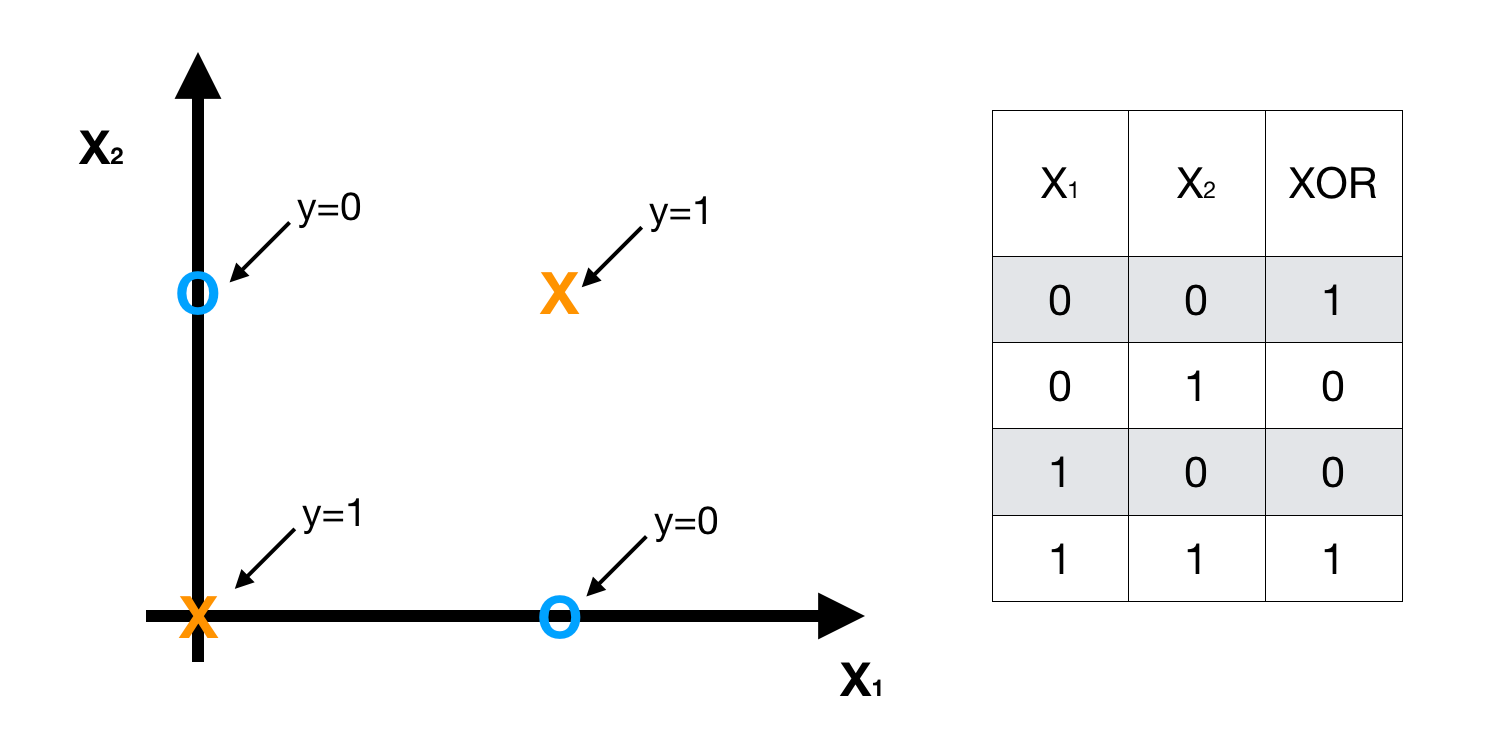


However, when the number of features and data is large, The H will be too complex to understand and the computation cost is expensive. Instead, we use NN structure to make model H more clear and simple. Here, we **apply NN to XOR Problem based on AND, NAND and OR.
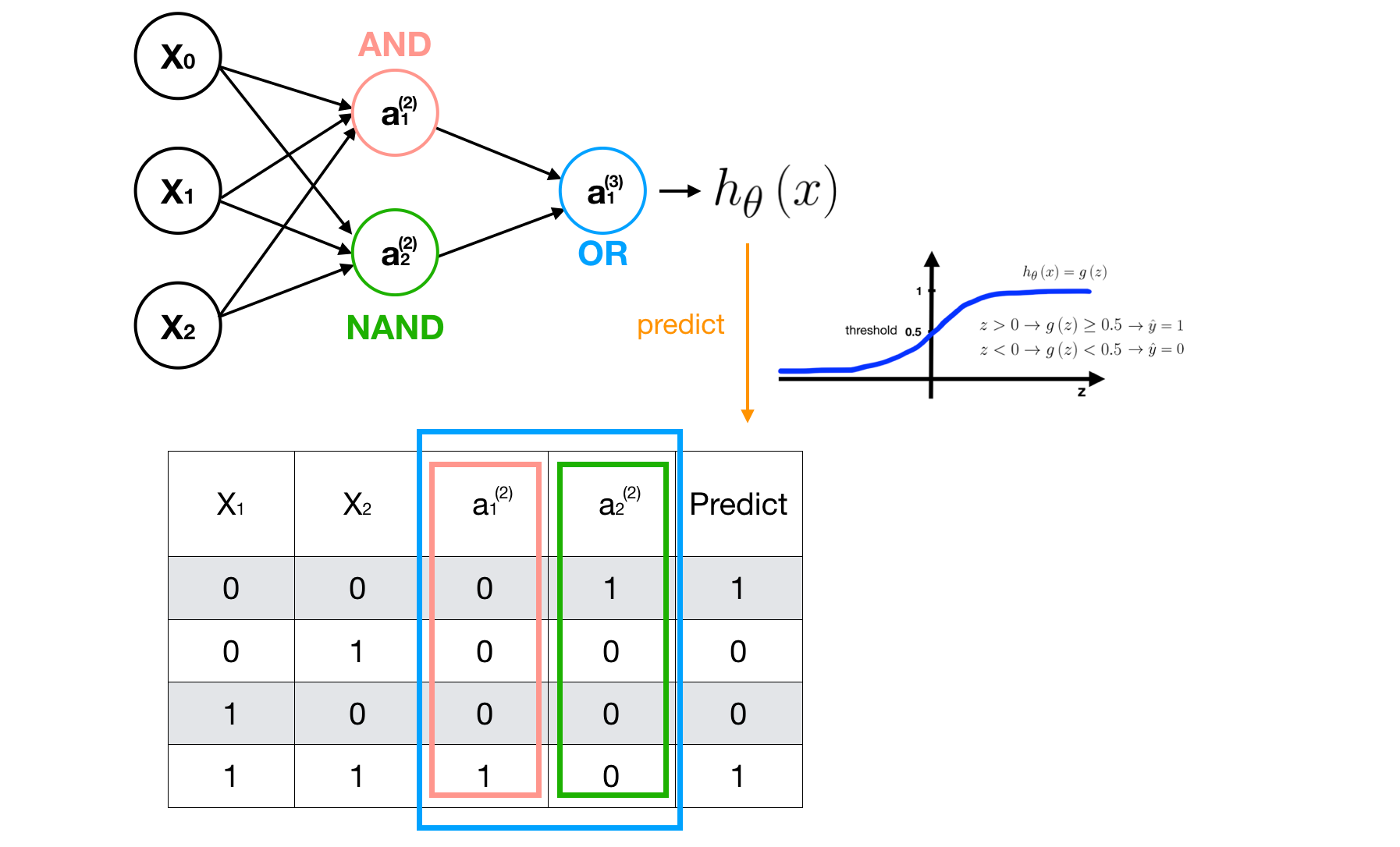
Multi-Class Classification Problem
In this case, we can add nodes in the Output Layer, each node can predict one class, the concept of this is similar to one-vs-all mechanism we discussed in week3.

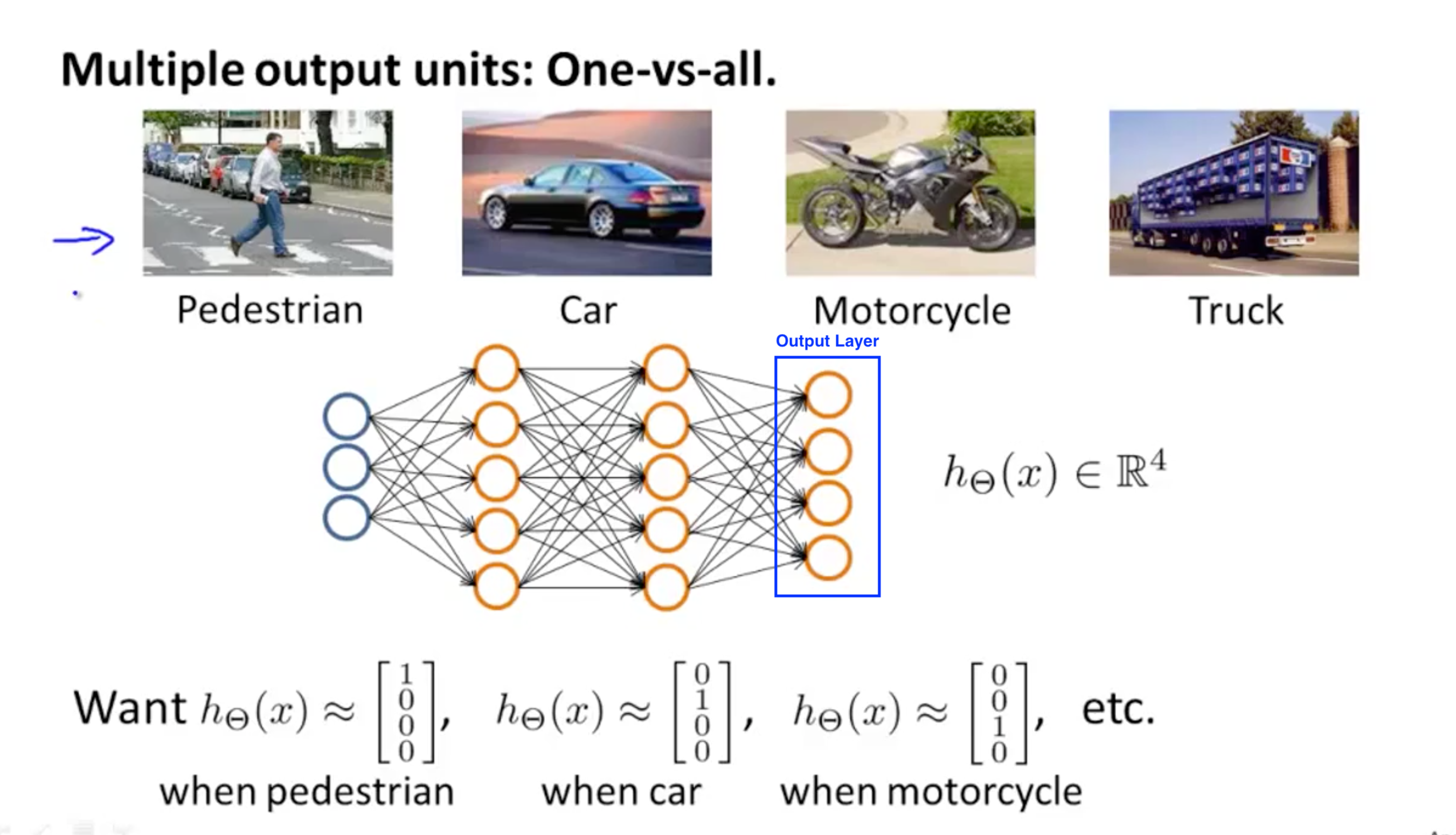
Source: week4 lecture slides, by Andrew Ng