Definition of Machine Learning
Machine learning is a science that gives computers the ability to learn without explicitly programmed.
Supervised Learning
given data with label (i.e. right answer)
(1) Regression Problem: predict continuous valued label
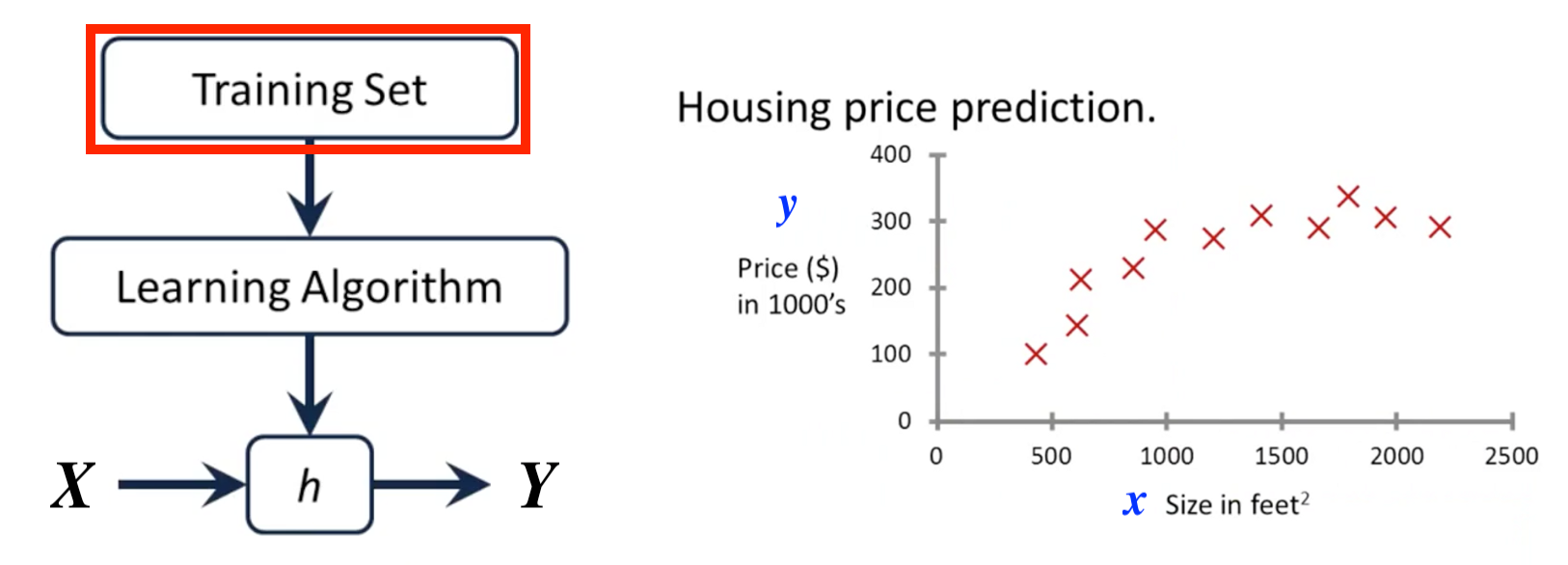
For example, given training data with housing size and price, which represents feature and label respectively. When new data comes in, our goal is to predict its label, that is, the corresponding value of housing price, in the range between [0, 400].


(2) Classification problem: predict discrete valued label
For example, given training data with tumor size and its category, which represents feature and label respectively. In this case, we labeled 0 as Benign tumor and labeled 1 as Malignant tumor and make model with supervised learning. When new data comes in, our training model predicts its label, that is, label 1 (Malignant) or label 0 (Benign).


Note: It’s called Binary or Binomial Classification if we group data in two kinds of label. It’s called Multi-class or Multinomial Classification if we group data in more than two kinds of label.
Unsupervised Learning
given data without any label(i.e. without any right answer)
Suppose each data has two features, denoted by x1 and x2. The biggest difference between supervised and unsupervised learning is that each data has a label in the case of supervised learning, whereas there is NO label for each data in the case of unsupervised learning, which means, they have not been classified.

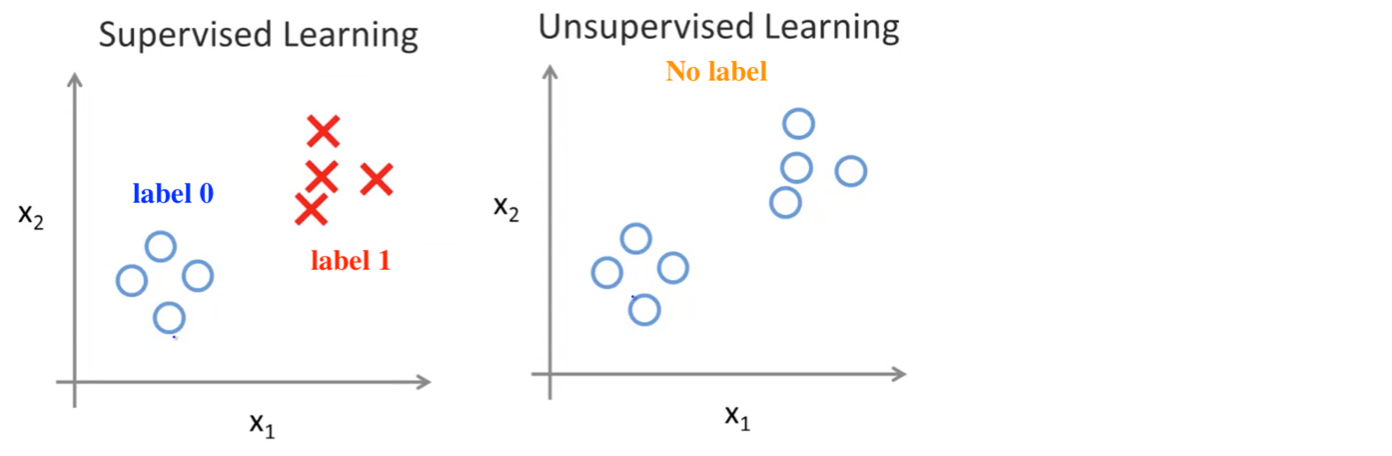
When we meet problems, should we apply Supervise Learning or Unsupervised Learning ?
Hint: For supervised learning, there will ALWAYS be an input-output pair. For unsupervised learning, there is just data with no label nor meaning and we try to make some sense out of it.
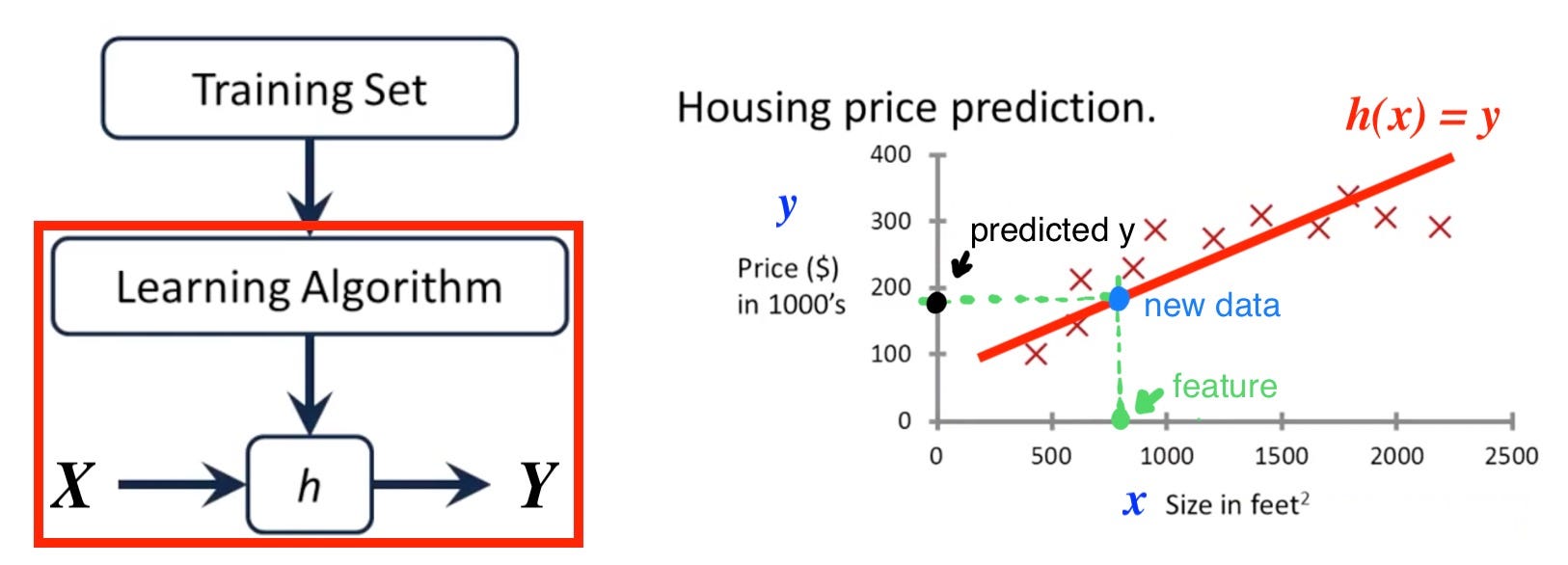
Making Model with Supervised Learning
Given a training dataset, making a model with supervised learning and fitting it by Learning Algorithm. In other words, learning a hypothesis function h: X → Y so that h(x) is a ‘good’ predictor for the corresponding value of y.

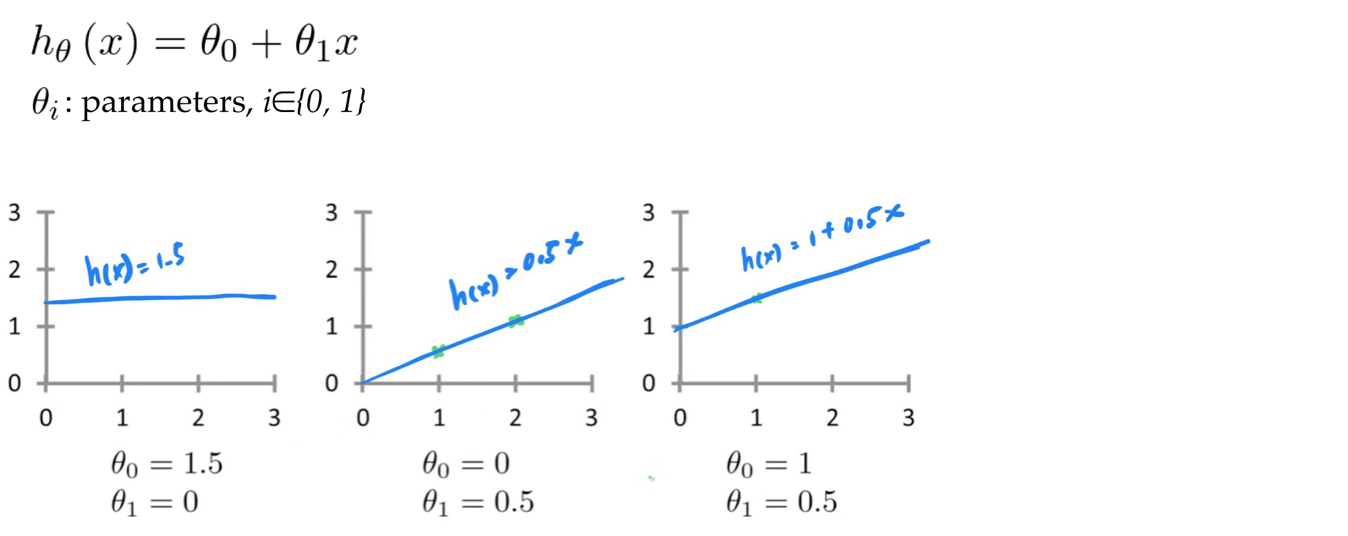
Linear Regression for Regression Problem
Linear Regression is a kind of hypothesis function
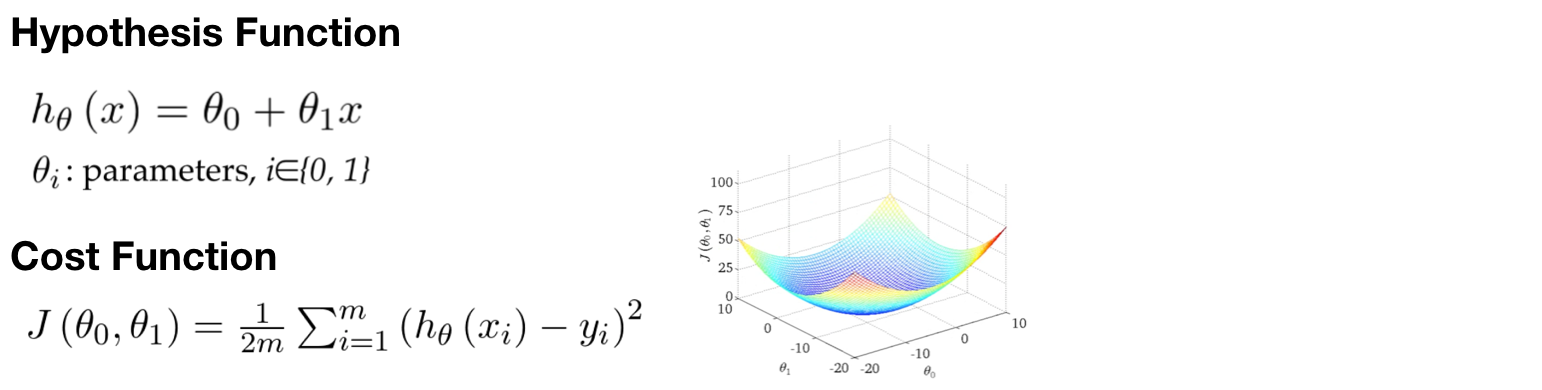
Linear Regression with one variable x and two parameters θ
Regression Problem: predict continuous valued label
Suppose we have a training dataset and each data is represented as (x, y). In Regression Problem, x ∈X is the feature and y∈Y is the continuous valued label.

After applying Learning Algorithm, our model will learn a hypothesis function h: X → Y so that h(x) is a ‘good’ predictor for the corresponding value of y.


When new data appears (blue point), we can predict its label (black mark) by its feature(green mark).
Cost Function
The accuracy of Hypothesis Function can be measured by using Cost Function.
Here, we use Square Error Function, one of the Cost Function, to measure the accuracy of Hypothesis Function.
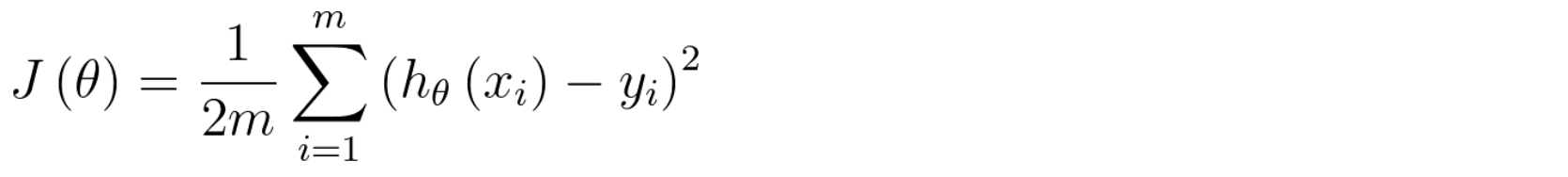
J(θ): cost function θ: parameters of the hypothesis function h(x) h(x): predicted label of data i y: actual label of data i m: amount of data
For example, suppose there is a Linear Regression with one variable and two parameters θ, the square error function will be as below

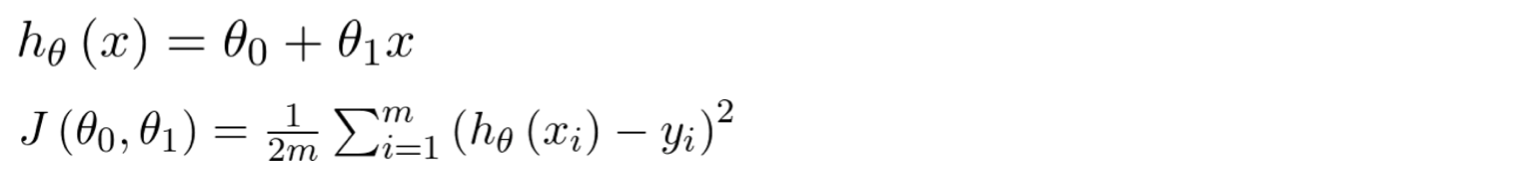
In the following figures, we can see what does Hypothesis Function and Cost Function look like.

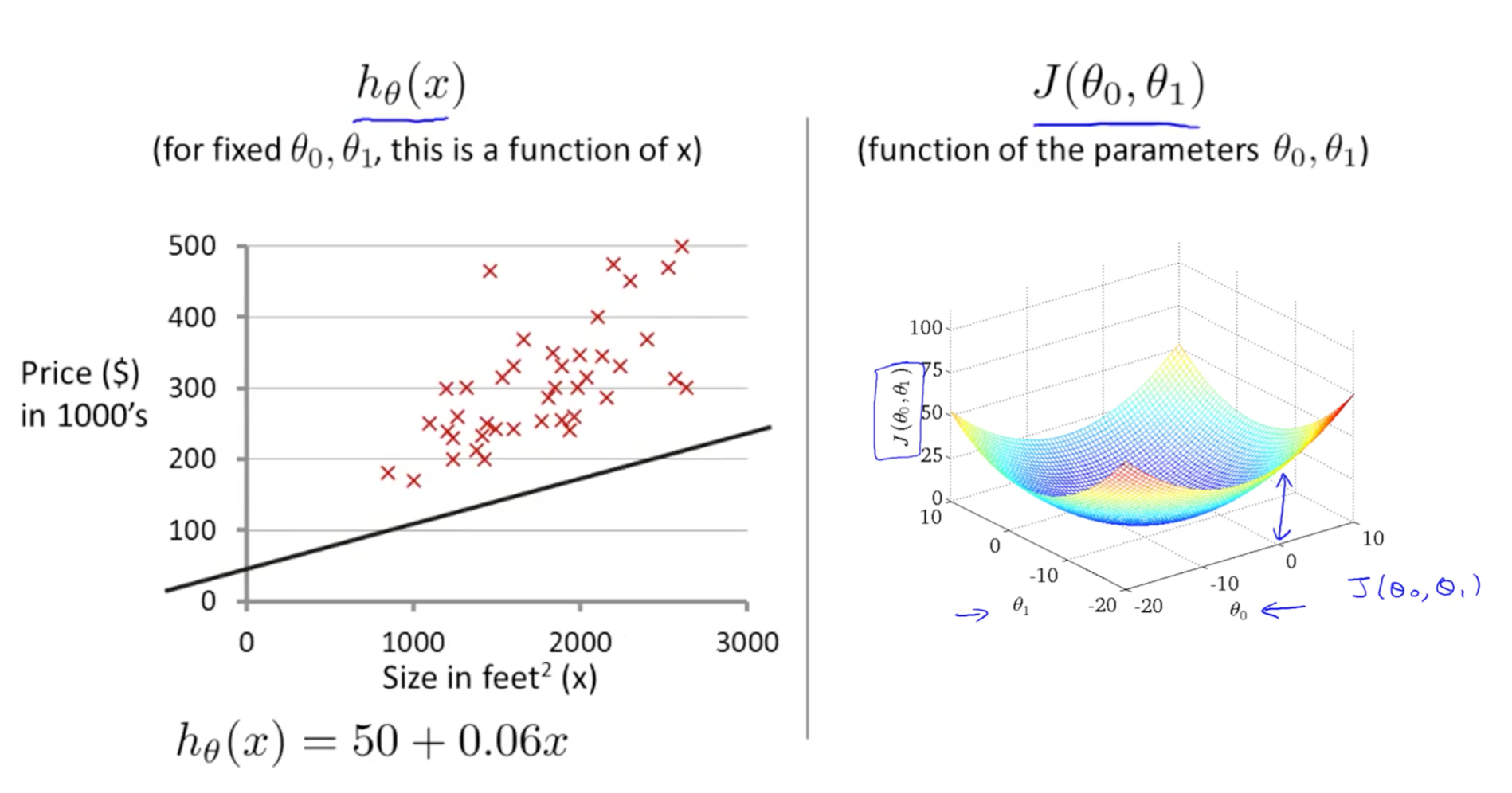
Our goal is to minimize the cost function!!
Gradient Descent Algorithm
Using Gradient Descent Algorithm to minimize the cost function.
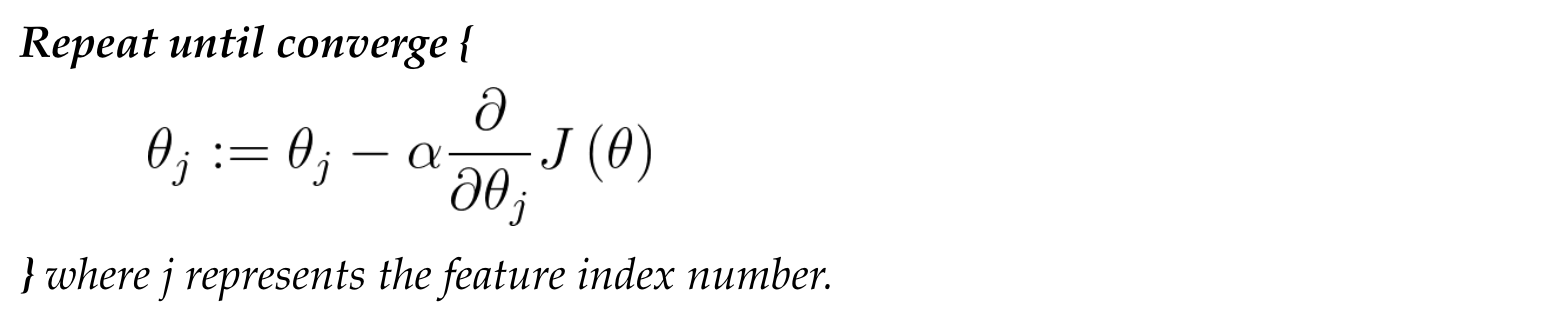
Note: Parameters θ should be simultaneously update at each iteration.
For example, applying Gradient Descent Algorithm to square error function.

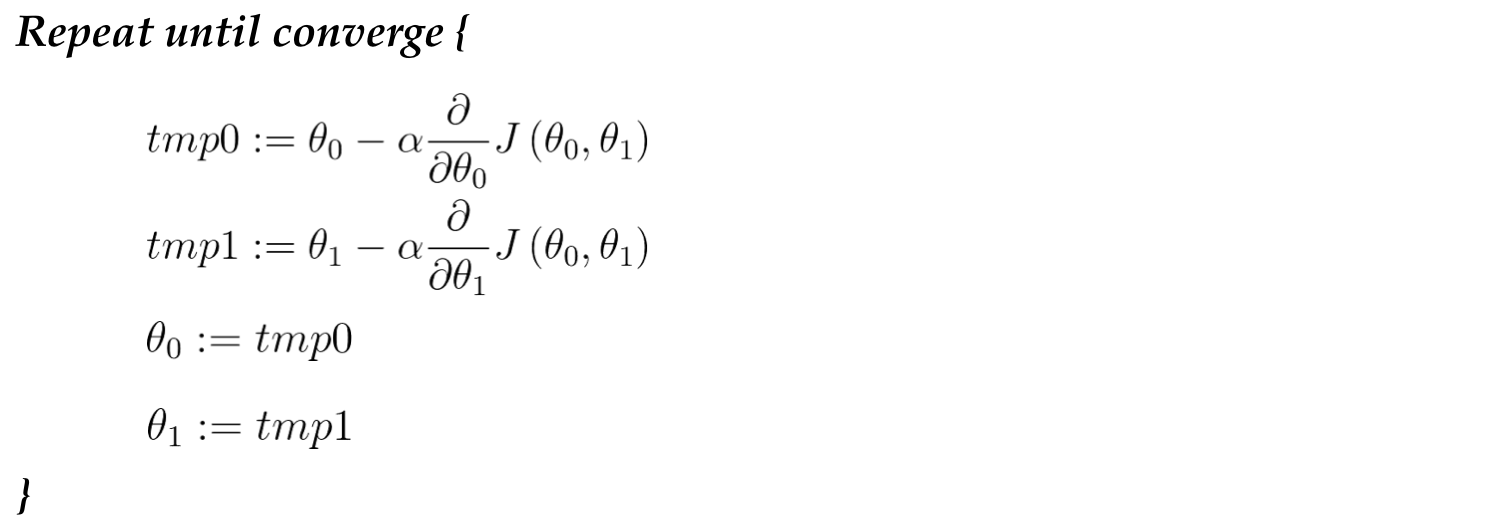
Note. Gradient Descent is called ‘batch’ gradient descent if it needs to look at every example in the entire training set at each step.
Learning Rate α
If **α is too small, Gradient Descent is slow. If α is too large, Gradient Descent may overshoot minimum and not converge.


Note: Choosing a proper learning rate α in the beginning and stick to it at each iteration since Gradient Descent will automatically take smaller steps when approaching local minimum.
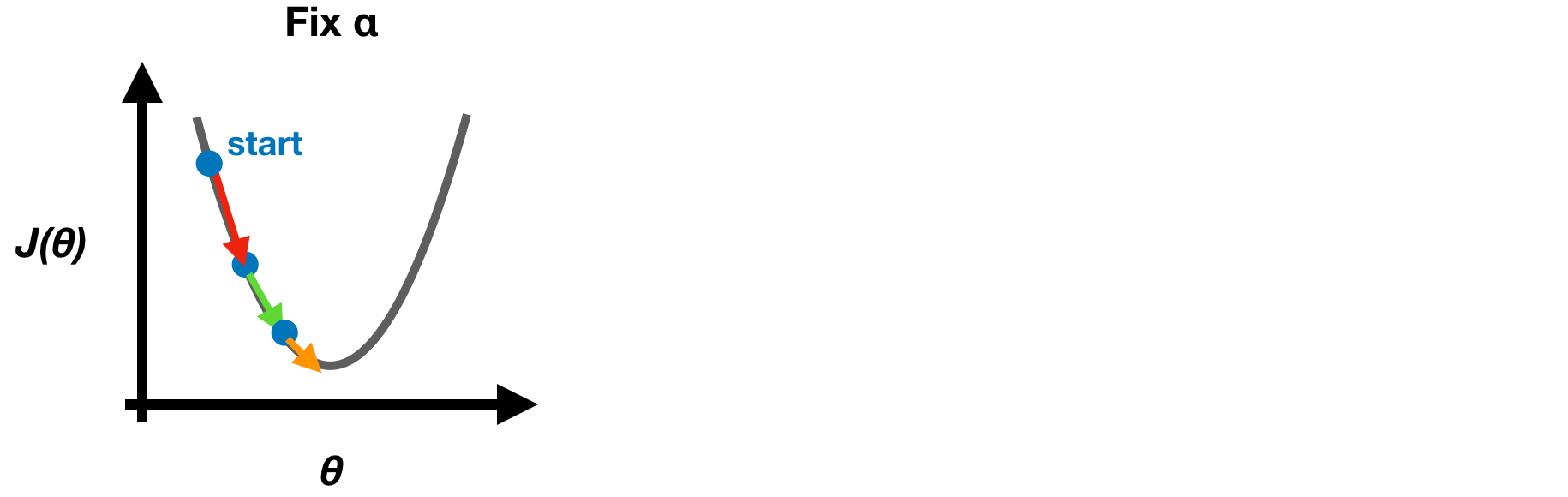
Gradient Descent for Linear Regression — at
Intuitive view
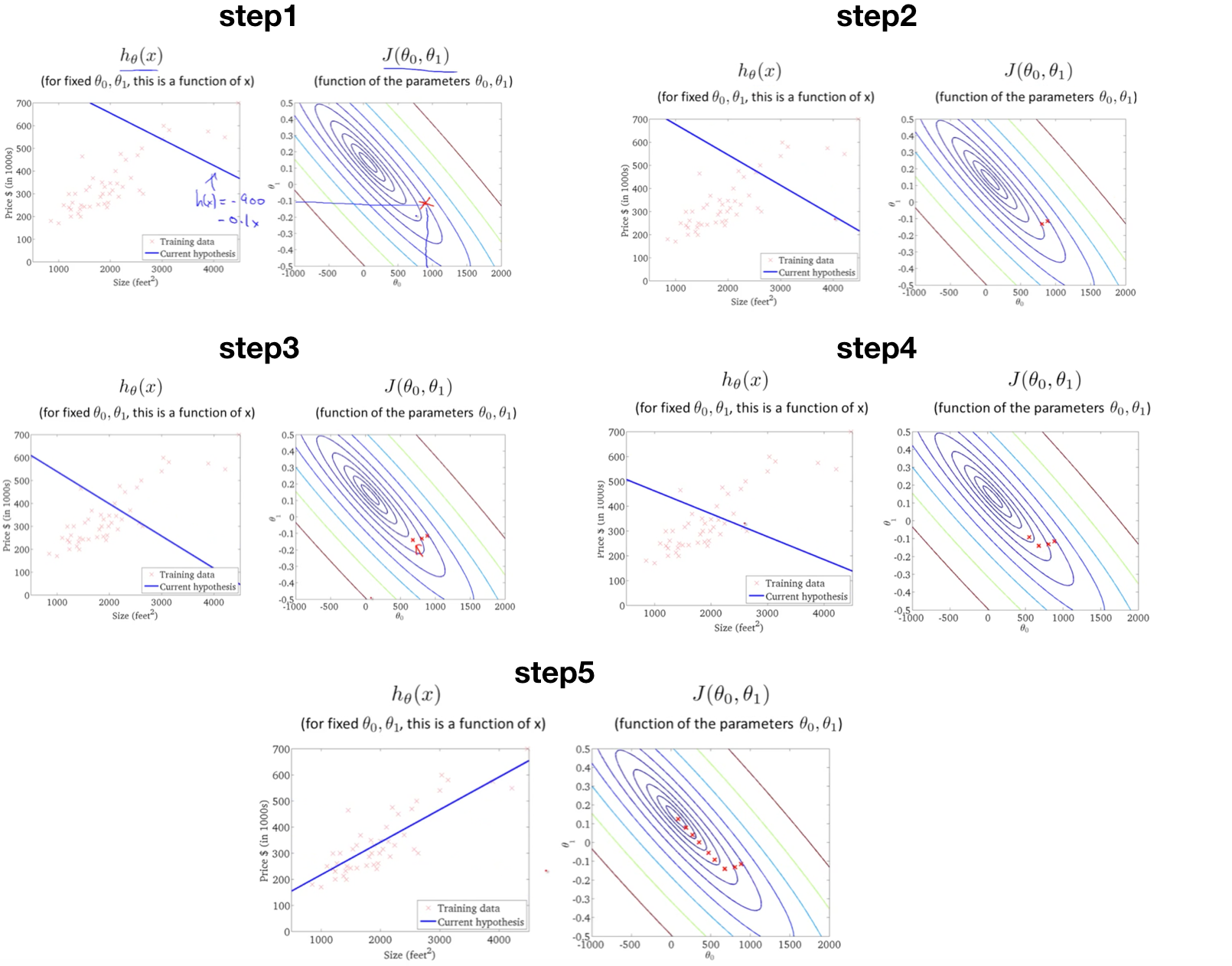
Applying Gradient Descent to minimize cost function and we can see what happens at each iteration, step1 to step 5. Ultimately, we will get a good hypothesis function with parameters θ.


In this note, we mainly focused on Linear Regression for Regression Problem and will discuss Logistic Regression, another kind of hypothesis function for Classification Problem, in ‘Machine Learning Notes — Week3’.





 Using Mockito for Java Unit Testing
Using Mockito for Java Unit Testing